群論の可視化とは

ブラウザの計算力のみで具体例を計算

実際に理論通り計算できている様子を観察

ルービックキューブなどの 3D モデルに具体的に適用する

とにかく群論を身近に感じてもらえるようにしたい

JavaScript で Computational Group Theory を実装するには

置換群 -> Schreier-Sims

群の表示 -> coset enumeration

有限体上の行列群 -> 置換群に焼き直し, Schreier-Sims

有限生成アーベル群 -> 整数環上の行列の Smith normal form

お題目

4x4x4 の rubik's cube と 24 puzzle の solver の実際の動作

coset enumeration の実際の動作

Schreier-Sims の実装

Minkwitz の方法の実装

以上のブラウザ上の実装を紹介

Rubik's cube puzzle と 24 puzzle をやってみよう

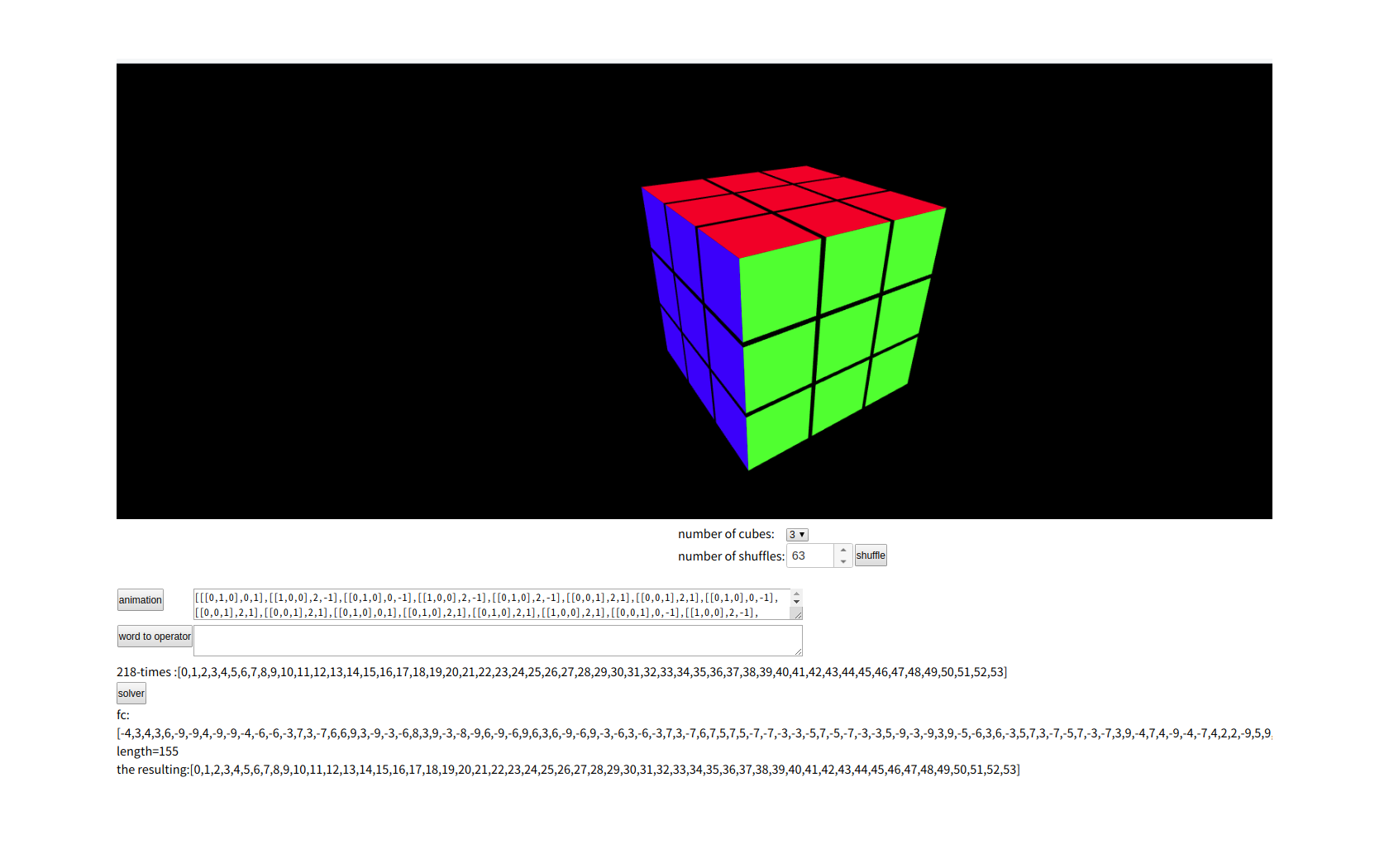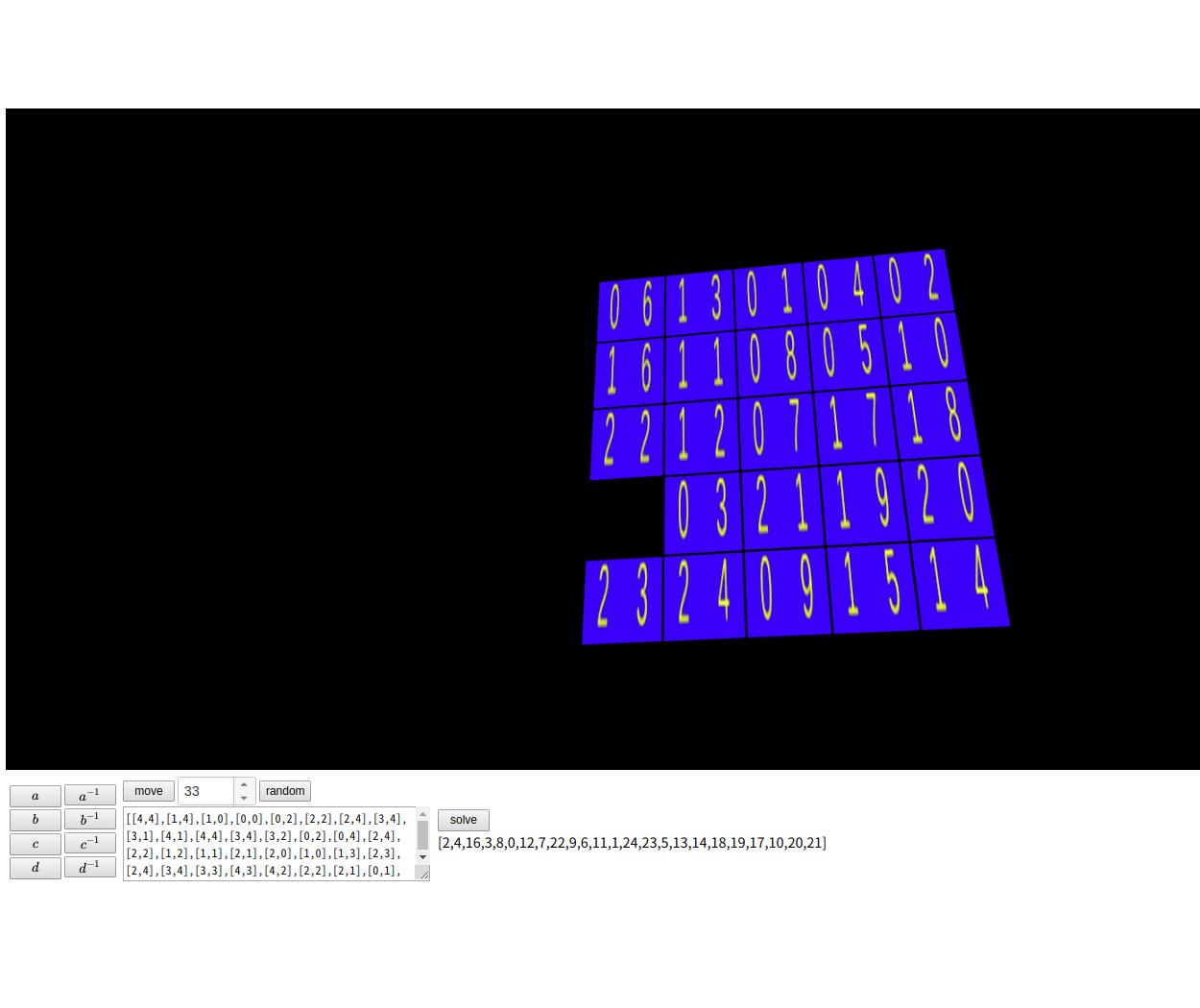coset enumeration とは

• 計算群論の教科書の定番であり, 手計算では失敗することが多い
• $\langle a,b\ |\ a^3,\ b^5,\ (ab)^2\rangle$
• 

coset enumeration をやってみよう

よく知られているように, coset enumeration では, 群の位数だけの行数が必要となる

von Dyck 群 $D(l,m,n) = \langle a,b\ |\ a^l,\ b^m,\ (ab)^n\rangle$

一般に, $\frac{1}{l}+\frac{1}{m}+\frac{1}{n}>1$ $\Rightarrow$ $\sharp D(l,m,n)<\infty$

coset enumeration (step by step)

coset enumeration (一気に)

ca.js とは

JavaScript の多倍長整数ライブラリ big-integer.js のみを利用した

自作数式処理ライブラリ

web ブラウザの計算能力のみで計算したい

2016年頃から作り始める

元々自身の知的探究と数式処理の教科書の勉強のためにJSを利用したことが動機

SymPy もライブラリを利用せず Python のみで書かれており, 目標が共通

具体的に何をしてきたのか

• 風呂敷を広げて回収(背伸びして何とか形にする)
• Pell 方程式 [00-07]
• groebner 基底 [05-12]
  (丸山正樹著 「グレブナー基底とその応用」 p82 「性能の低い計算機代数のソフトでは相当待っても答えが出ない」)
• 単因子計算 [13-02]
• Jordan 標準形計算 [13-03]
• Hensel 構成による因数分解 [02-15, 02-21]
• Schreier-Sims アルゴリズム [15-11] など
• Minkwitz factorization [15-15, 15-16] など
• coset enumeration [16-00] など

Schreier-Sims Algorithm とは

• BSGS を求める方法
• BSGS = Base + Strong Generating Set
• 有限集合 $\Omega$ 上の対称群を $\mathfrak{S}_{\Omega}$ と表す
• 特に $\Omega=\{0,1,\cdots,n-1\}$ のときは $\mathfrak{S}_n$ と表す
• 以下では $G=\langle X \rangle \leq \mathfrak{S}_n$ とする
• Base $B = (b_0, \cdots, b_s)$ $b_0,\cdots,b_s\in\{0,1,\cdots,n-1\}$に対し
• $G=\prod_{i=0}G_{\{b_0,\cdots,b_i\}}\backslash G_{\{b_0,\cdots,b_{i-1}\}}$ と集合で表す方法
• これを JavaScript で実装した ca.js [15-05~15-08]

Schreier-Sims Algorithm の困難

• $i$ が増えるに連れ $G_{\{b_0,\cdots,b_i\}}$ の生成系が雪だるま式に肥大化
• $\rightarrow$ ブラウザが簡単にクラッシュ
• それを解消する手段として Jerrum's filter を用いた
• $G_{\{b_0,\cdots,b_i\}}$ の位数を $n$ 以下に抑えることができる
• cycle を潰し, spanning tree にするグラフ理論的方法
• ca.js [15-11]

Schreier-Sims Algorithm だけでは permutation puzzle は解けない

• Minkwitz の方法
• strong generating set をオリジナルの生成系とその逆元の語で表示する方法
• オンラインの論文(理解できない)を見て, 無理やり実装
• 正直正しいものかどうかどうか怪しいが一応実装できた
• ca.js [15-16]
• Minkwitz の論文は7ページと短く, 群の表示に関して掘り下げた議論が見いだせない

BSGS の導出は時間が掛かる

• A24 (24 puzzle) の生成には標準的なノートPCで30秒ほどかかる
• 3x3x3 の rubik's cube では 3 ~ 4 分ほどかかる!
• 4x4x4 の rubik's cube では 16 時間ほどかかる!
• しかし, 一度 BSGS を求めてしまえば, それを利用して solver を実装することは容易で,
• JavaScript であっても負荷が少ない.

Rubik's cube をブラウザに実装したくなる

• Three.js を使おう　
• 和島茂先生のサイトに感銘を受ける
• 遠藤理平氏のサンプルコードから頑張って自力で実装
• 4x4x4 までの rubik's cube で Minkwitz の方法が一応上手く働いた

今後の目標

Rust と webassembly の習得

Minkwitz の論文では, 語の長さが主題であるにも関わらず, 群の表示や項書き換えについて触れていない

置換群 $G = \langle g_1,\cdots,g_m\rangle \leq \mathfrak{S}_{\Omega}$ から $G\simeq \langle x_1,\cdots,x_m | r_1,\cdots ,r_k\rangle$ となる表示を得る方法について掘り下げる

部分群の表示を与える Reidemeister-Schreier アルゴリズムの実装

Knuth-Bendix の項書き換えアルゴリズムの実装