JavaScript で CGT
@日本数式処理学会第30回大会
2021年6月6日
松川信彦
大阪教育大学附属池田中学校
https://noblegarden-math.jp/math/CGT
| computational group theory | ->計算機群論 |
| 主な対象 : 置換群($\leq \mathfrak{S}_n$) | |
| 主な方法 : Schreier-Sims | |
| combinatorial group theory | ->組合せ論的群論 |
| 主な対象 : 群の表示 | |
| 主な方法 : coset enumeration |
JavaScript で群を実装するには
置換群 -> Schreier-Sims
群の表示 -> coset enumeration, Knuth-Bendix, Groebner-Shirshov, Newman's (Diammond) lemma
有限体上の行列群を置換群に焼き直したものに Schreier-Sims
有限生成アーベル群 -> 整数環上の行列の Smith normal form
お話しする内容:
Schreier-Sims アルゴリズムの簡単な解説
Minkwitz factorization の動作
4x4x4 の rubik's cube と 24 puzzle の solver の実際の動作
Reidemeister-Schreier, modified coset enumeration の動作
課題
Schreier's lemma
- 部分群の生成系を与える, 簡単ではあるが基本中の基本で重要な補題
- $G=\langle X\rangle$, $H\leq G$, $T$:$G$ における $H$ の右剰余類分解の完全代表系
- $G\rightarrow T\quad (\sigma \mapsto \overline{\sigma})$ を $H\sigma = H\overline{\sigma}$ なる写像とするとき
- $H=\langle tx\overline{tx}^{-1}\ |\ t\in T,\ x\in X\rangle$
Schreier-Sims Algorithm とは
- BSGS を求める方法
- BSGS = Base + Strong Generating Set
- 有限集合 $\Omega$ 上の対称群を $\mathfrak{S}_{\Omega}$ と表す
- 特に $\Omega=\{1,\cdots,n\}$ のときは $\mathfrak{S}_n$ と表す
- 以下では $G=\langle X \rangle \leq \mathfrak{S}_n$ とする
- Base とは $B = (b_1, \cdots, b_s)$ $(b_1,\cdots,b_s\in\{1,\cdots,n\})$ であって
- $G^{(i)}:=G_{b_1,\cdots,b_i}$ ($G^{(0)}:=G$) とおくとき
- $G^{(s-1)}\neq 1$ であるが, $G^{(s)}=1$ となるもの.
- $G=\prod_{i=0}^{s-1}G^{(i+1)}\backslash G^{(i)}$ と集合で表す方法
- $G^{(i+1)}\backslash G^{(i)}\simeq b_{i+1}^{G^{(i)}}$ はサイズが小さいから, 大きくなりがちな置換群において, 基底のような役割を演ずる.
Schreier-Sims Algorithm の困難
- $i$ が増えるに連れ Schreier's lemma によって構成される $G^{(i)}=G_{\{b_0,\cdots,b_i\}}$ の生成系は雪だるま式に肥大化する.
- $\rightarrow$ 何の工夫も施すことがなければブラウザは簡単にクラッシュ
- それを解消する手段として Jerrum's filter を用いる
- Jerrum's filter は $\mathfrak{S}_n$ の任意の部分群に対し, その生成系の大きさが $n-1$ 以下で抑えられることを証明するだけではなく, 具体的に実装することのできるアルゴリズム.
- $H=\langle X\rangle\leq \mathfrak{S}_n$ を任意の部分群とするとき, $\sigma\in X$ に対し, $i\neq i^{\sigma}$ となる最小の $i$ に対し $\{i,i^{\sigma}\}$ を辺とする無向グラフを作り,
- そのグラフから閉路を潰し, 木 (辺の数は $n-1$ 以下になる)にするグラフ理論的方法
Schreier-Sims Algorithm だけでは permutation puzzle は解けない
- Minkwitz の方法
- strong generating set をオリジナルの生成系の語として表示する方法
- Minkwitz の原論文を見て, (怪しいが) 一応実装できた
- JSによる実装の紹介
- JSによる実装の紹介(有限行列群への応用)
- Minkwitz の方法は実用的ではあるが, 原論文は7ページと短く, 群の表示, 項書換えに関して掘り下げた議論が見いだすことができなかった.
Rubik's cube puzzle と 24 puzzle の動作
 |
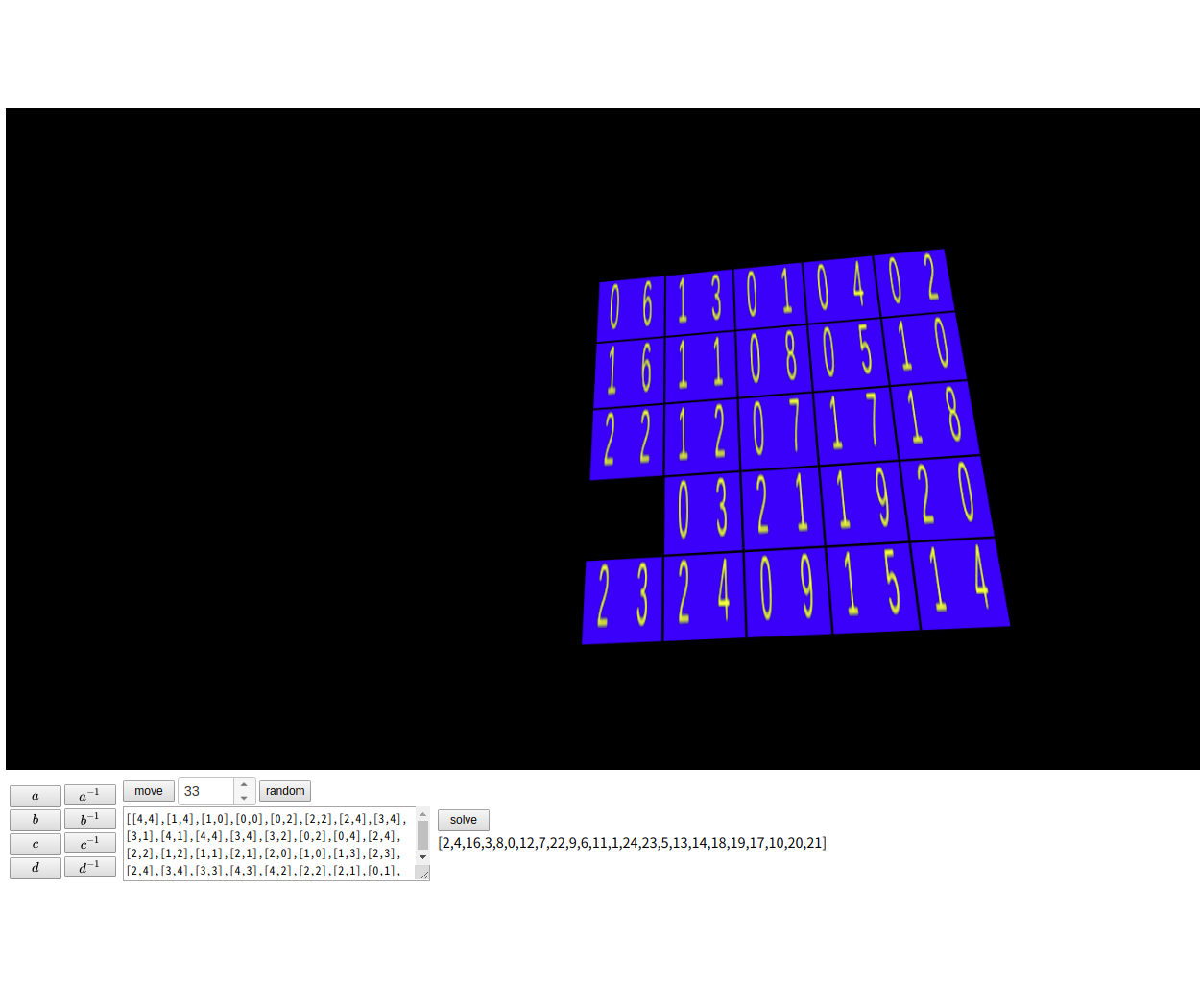 |
BSGS の導出は時間が掛かる
- A24 (24 puzzle) の生成には標準的なノートPCで30秒ほどかかる
- 3x3x3 の rubik's cube では 3 ~ 4 分ほどかかる!
- 4x4x4 の rubik's cube では 16 時間ほどかかる!
- BSGS(+Minkwitz)は置換パズルの鍵なので solver の実装は鍵を使ってドアを開くだけの作業にすぎず, JavaScript であっても容易に実装でき, しかも負荷が少ない.
- BSGS の導出および Minkwitz 分解は鍵の鋳造にあたるので高コスト高負荷.
coset enumeration
有限集合 $X$ と, それを生成系とする自由群 $F(X)(\simeq \underset{|X|\text{ times}}{\underbrace{\mathbb{Z}\ast \cdots \ast \mathbb{Z}}})$ と
有限部分集合 $R\subseteq F(X)$ が与えられ, $F(X)$ における $R$ の正規閉包を $\mathrm{NC}_{F(X)}(R)$ と表したとき, $F(X)/\mathrm{NC}_{F(X)}(R)$ を $\langle X\ |\ R\rangle$ と表し, これを群の表示という.
$X$ をgenerator, $R$ をrelator という.
$G=\langle X\ |\ R\rangle$ と, その部分群 $H$ を $[G:H]<\infty$ なるものとする.
準同型 $G\rightarrow \mathfrak{S}_{H\backslash G}$ を構成するアルゴリズムのこと.
特に $H=1$ のとき, $G\rightarrow \mathfrak{S}_G$ なので, 位数の大きい群では適切に部分群を選ぶ技術が必要である.
coset Enumeration ( + Reidemeister-Schreier) の実装
$G=\langle X\ |\ R\rangle$, $H\leq G$ を $[G:H]<\infty$ なるものとする.
$[G:H]<\infty$ だから $H$ の $G$ における Schreier transversal $T$ が構成でき, そこから
$G\rightarrow T\quad (\sigma\mapsto \overline{\sigma})$ を $H\sigma = H\overline{\sigma}$ なるものとし
$\widehat{Y}:=\{y_{t,x}\ |\ t\in T,\ X\in X,\ tx\neq \overline{tx}\}$, $S:=\{\rho_t(w)\ |\ t\in T,\ w\in R\}\subseteq F(\widehat{Y})$ とおくとき
$H$ は $\widehat{Y}$ を generator, $S$ を relator とする表示をもつ. すなわち $H\simeq \langle \widehat{Y}\ |\ S\rangle$ となる.
modified coset Enumeration
部分群の生成系が与えられたとき. 例えば $H=\langle Y\rangle \leq G=\langle X\ |\ R\rangle$ であるとき,
$\widehat{Y}$ を $Y$ と bijective な集合とし, $H\simeq \langle \widehat{Y}\ |\ S\rangle$ なる $S\subseteq F(\widehat{Y})$ を構成するアルゴリズム.
課題と目標
Rust(or C++) と webassembly による web における高速化のための実装
Schreier-Sims の高速化 (Rubik's cube 群の計算は 4*4*4 が限界)
coset enumeration 高速化 (複素鏡映群くらいなら何とか計算できるが, 指数が 10000 を超えるとしんどい)
Reidemeister-Schreier や modified coset enumeration における関係式の simplification.
BSGS から群の表示を構成する Cannon (CONSTRUCTION OF DEFINING RELATORS FOR FINITE GROUPS 1973) のアルゴリズムの実装.
Knuth-Bendix や Groebner-Shrishov などの非可換代数との関連を探究する.